Harmony and Grid Symmetry
An audio-visual link between musical harmony and symmetries of a grid
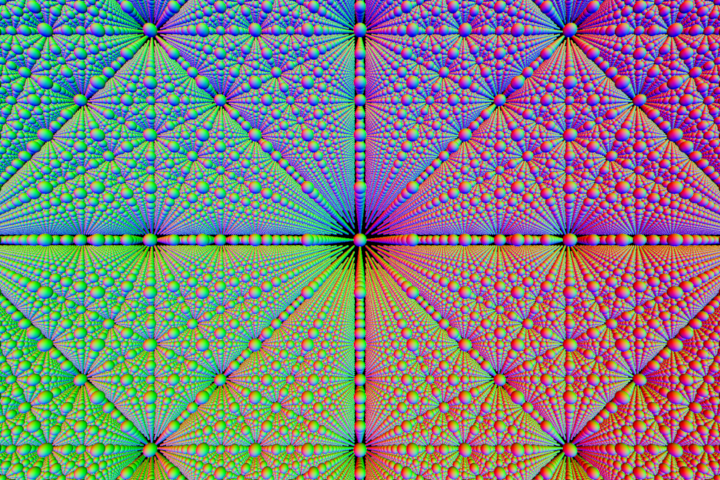
Motivation
This idea came about when I messing about with raymarching, where it is easy to render an infinitely repeating grid of objects, and I noticed that these geometric paterns emerged that seemed to line up with directions that had a simple ratio of x:y:z. You know what else kind of corresponds to simple ratios? Musical harmony!
In this article I aim to show you that the patterns you see in the image above correspond in some way to musical chords. The key point here is that both come from simple ratios of integers.
Musical intervals
In music, a gross oversimplification is to say that intervals with a simple ratio of frequencies sound consonant, whilst less simple ratios tend to sound more dissonant. For example, a perfect 5th is a very consonant sounding interval and has frequency ratio 2:3. On the other hand, something like a tritone has frequency ratio 32:45. You can compare the 2 sounds below.
[TODO: INSERT SOUND THINGS HERE]Symmetric patterns
Certain points in the image stand out more than others, as a whole bunch of spheres line up behind one another. I have highlighted a few of these points below.
Each point on the image represents some direction in 3D space. The point "A" in the center of the image for example is the cameras forward direction, written as a row vector (0, 0, 1). Whereas the point "B" corresponds to the direction (-0.5, 0, 1), and "C" is to the direction (-0.4, 0.2, 1). We can scale each of these direction vectors so that they have integer components, allowing us to look at the ratios of their components.
A is still just (0, 0, 1), giving ratio 0:0:1.
B scales up to give (-1, 0, 2). We dont care about the negative, so we end up with ratio 1:0:2.
C scales up to give (-2, 1, 5), giving ratio 2:1:5.